Exercícios sobre Juros Compostos
Problema: João investiu R$ 10.000,00 em uma aplicação que rende juros compostos a uma taxa de 8% ao ano. Quanto ele terá ao final de 3 anos?
Solução: Utilizando a fórmula do montante com juros compostos:
M = P * (1 + r)t
Onde:
M = Montante (valor final),
P = Principal (valor inicial),
r = Taxa de juros em decimal,
t = Tempo em anos.
Substituindo os valores:
M = 10000 * (1 + 0.08)3
M = 10000 * (1.08)3
M = 10000 * 1.259712
M ≈ 12597,12
Portanto, João terá aproximadamente R$ 12.597,12 ao final de 3 anos.
Problema: Maria investiu R$ 5.000,00 em uma aplicação que rende juros compostos a uma taxa de 6% ao ano. Quanto ela terá ao final de 5 anos?
Solução: Utilizando a mesma fórmula do montante com juros compostos:
M = P * (1 + r)t
Substituindo os valores:
M = 5000 * (1 + 0.06)5
M = 5000 * (1.06)5
M = 5000 * 1.338225
M ≈ 6691,12
Portanto, Maria terá aproximadamente R$ 6.691,12 ao final de 5 anos.
Problema: Pedro investiu R$ 8.000,00 em uma aplicação que rende juros compostos a uma taxa de 10% ao ano. Quanto tempo levará para seu investimento dobrar?
Solução: Para encontrar o tempo necessário para dobrar o investimento, podemos reorganizar a fórmula do montante para resolver t:
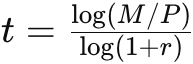
Onde log é o logaritmo na base 10.
Substituindo os valores:
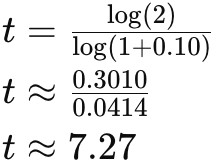
Portanto, levará aproximadamente 7,27 anos para o investimento de Pedro dobrar.
Problema: Ana investiu R$ 12.000,00 em uma aplicação que rende juros compostos a uma taxa de 5% ao ano. Quanto tempo levará para seu investimento triplicar?
Solução: Utilizando a mesma fórmula do problema anterior, para triplicar o investimento:
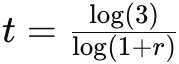
Substituindo os valores: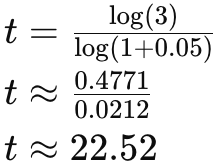
Portanto, levará aproximadamente 22,52 anos para o investimento de Ana triplicar.
Problema: Um empréstimo de R$ 7.000,00 foi contraído a uma taxa de juros compostos de 12% ao ano. Quanto tempo levará para o valor total a ser pago atingir R$ 10.000,00?
Solução: Utilizando a mesma fórmula do montante com juros compostos, isolando o tempo:
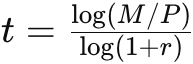
Substituindo os valores:
Portanto, levará aproximadamente 3,15 anos para o valor total a ser pago atingir R$ 10.000,00.
Esses exercícios fornecem uma prática básica para entender e aplicar os conceitos de juros compostos.
